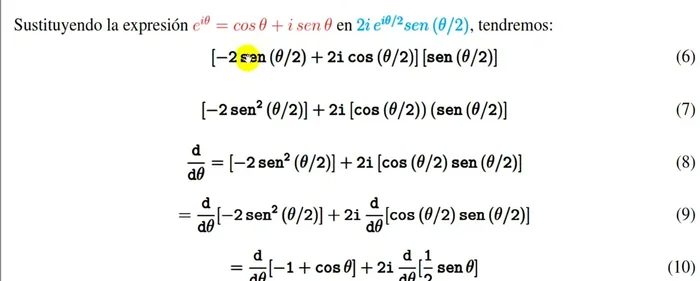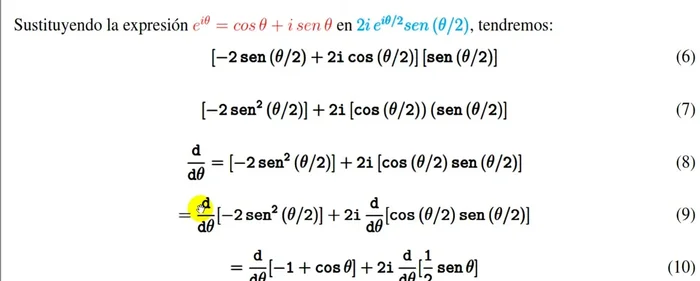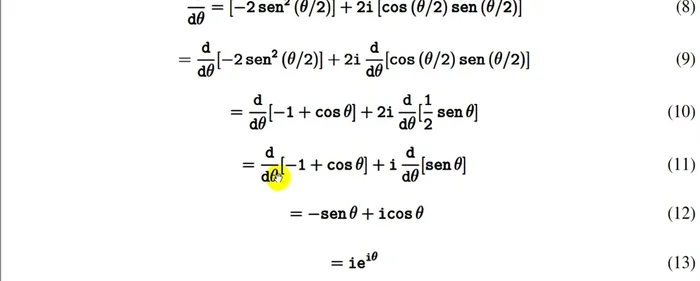Derivación de Números Complejos: Método Eficaz con Wolfram Alpha

Updated at: 26/06/2025

Differentiating complex numbers can be tricky, but it doesn't have to be! This article explores a streamlined method for deriving complex functions, leveraging the power of Wolfram Alpha. We'll guide you through the process step-by-step, showing you how to use Wolfram Alpha's capabilities to simplify complex differentiation problems and obtain accurate, quick results. Say goodbye to tedious calculations and hello to efficient complex analysis.

Instrucciones Paso a Paso

  1. Derivación del término izquierdo

    • e^(iθ) - 1
    • Sustituir la expresión e^(iθ) = cos(θ) + i sen(θ) en el término de la izquierda.
    • Derivar la expresión resultante con respecto a θ. Utilizar reglas de derivación para coseno y seno.
    • i * e^(iθ).
    Simplificar la derivada para obtener el resultado: i * e^(iθ). Simplificar la derivada para obtener el resultado: i * e^(iθ). Simplificar la derivada para obtener el resultado: i * e^(iθ). Simplificar la derivada para obtener el resultado: i * e^(iθ).
    Derivación del término izquierdo
    • Verificar el resultado con Wolfram Alpha. Introducir la expresión original e^(iθ) - 1 y obtener su derivada.
    Verificar el resultado con Wolfram Alpha. Introducir la expresión original e^(iθ) - 1 y obtener su derivada.
    Derivación del término izquierdo

  2. Derivación del término derecho

    • 2i * e^(iθ/2) * sen(θ/2)
    • Sustituir la expresión e^(iθ) = cos(θ) + i sen(θ) en el término de la derecha.
    • Realizar el producto y simplificar la expresión.
    • Derivar la expresión resultante con respecto a θ. Utilizar reglas de derivación y simplificaciones trigonométricas (identidades).
    Derivar la expresión resultante con respecto a θ. Utilizar reglas de derivación y simplificaciones trigonométricas (identidades). Derivar la expresión resultante con respecto a θ. Utilizar reglas de derivación y simplificaciones trigonométricas (identidades). Derivar la expresión resultante con respecto a θ. Utilizar reglas de derivación y simplificaciones trigonométricas (identidades). Derivar la expresión resultante con respecto a θ. Utilizar reglas de derivación y simplificaciones trigonométricas (identidades).
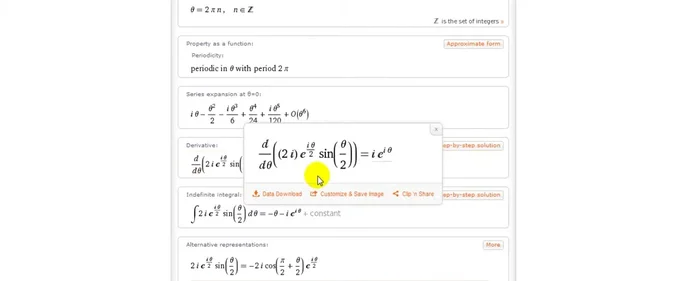
    Derivación del término derecho
    • i * e^(iθ).
    • Verificar el resultado con Wolfram Alpha. Introducir la expresión original 2i * e^(iθ/2) * sen(θ/2) y obtener su derivada.
    Verificar el resultado con Wolfram Alpha. Introducir la expresión original 2i * e^(iθ/2) * sen(θ/2) y obtener su derivada. Verificar el resultado con Wolfram Alpha. Introducir la expresión original 2i * e^(iθ/2) * sen(θ/2) y obtener su derivada.
    Derivación del término derecho

  3. Comparación de resultados

    • Comparar los resultados obtenidos para el término de la izquierda y el término de la derecha. Ambos deben ser iguales a i * e^(iθ).
    Comparar los resultados obtenidos para el término de la izquierda y el término de la derecha. Ambos deben ser iguales a i * e^(iθ).
    Comparación de resultados
[RelatedPost]

Tips

  • Utilizar Wolfram Alpha para verificar los resultados y entender el proceso paso a paso.
  • Recordar las identidades trigonométricas para simplificar las expresiones.
  • Practicar con otros ejemplos similares para dominar la técnica.

Common Mistakes to Avoid

1. Error en la conjugación compleja

Razón: Se olvida o se aplica incorrectamente la conjugación del denominador al racionalizar expresiones con números complejos.
Solución: Recuerda que para racionalizar, se multiplica el numerador y el denominador por el conjugado del denominador.

2. Confusión con las operaciones de suma y multiplicación

Razón: Se suman o multiplican incorrectamente las partes real e imaginaria de los números complejos, olvidando las reglas específicas de cada operación.
Solución: Asegúrate de sumar las partes reales entre sí y las partes imaginarias entre sí, y aplicar la propiedad distributiva para la multiplicación.

FAQs

¿Puedo usar Wolfram Alpha para derivar funciones complejas con múltiples variables?
Sí, Wolfram Alpha puede manejar derivadas parciales de funciones complejas con varias variables. Simplemente introduce la función y especifica la variable con respecto a la cual deseas derivar. Por ejemplo, para la derivada parcial de f(z,w) = z²w con respecto a z, escribe 'D[z^2*w, z]'.
¿Qué pasa si Wolfram Alpha me da un resultado que no entiendo?
Si el resultado de Wolfram Alpha parece complicado, intenta simplificarlo usando las herramientas de simplificación que ofrece la plataforma. También puedes intentar reescribir la función original en una forma más sencilla antes de introducirla en Wolfram Alpha. Si aún tienes dudas, busca información adicional sobre las funciones o las técnicas de derivación involucradas.