Análisis de Varianza (ANOVA) de un Factor: Guía Completa con Ejemplo en SPSS

Updated at: 02/06/2025

El Análisis de Varianza de un factor (ANOVA) es una herramienta estadística poderosa para comparar las medias de tres o más grupos. Esta guía completa te enseñará los fundamentos del ANOVA, sus supuestos, y cómo realizar un análisis completo utilizando SPSS. Aprenderás a interpretar los resultados y a tomar decisiones basadas en la evidencia. Prepárate para dominar el ANOVA y extraer conclusiones significativas de tus datos.

Instrucciones Paso a Paso

  1. Introducción al ANOVA de un factor

    • Introducción al ANOVA de un factor. Se utiliza para comparar las medias de varios grupos independientes.
    Introducción al ANOVA de un factor. Se utiliza para comparar las medias de varios grupos independientes.
    Introducción al ANOVA de un factor

  2. Hipótesis y Supuestos

    • H0 (hipótesis nula): las medias de todos los grupos son iguales. H1 (hipótesis alternativa): al menos una media es diferente.
    • normalidad de los datos en cada grupo, homogeneidad de varianzas y grupos independientes.
    Supuestos del ANOVA: normalidad de los datos en cada grupo, homogeneidad de varianzas y grupos independientes. Supuestos del ANOVA: normalidad de los datos en cada grupo, homogeneidad de varianzas y grupos independientes.
    Hipótesis y Supuestos

  3. Ventajas del ANOVA sobre pruebas t múltiples

    • evita el aumento de la probabilidad de error tipo I.
    Ventajas del ANOVA sobre pruebas t múltiples: evita el aumento de la probabilidad de error tipo I.
    Ventajas del ANOVA sobre pruebas t múltiples

  4. Interpretación del ANOVA

    • Si el valor p (significancia) es menor a 0.05, se rechaza la hipótesis nula.
    • Representa la razón de la variación entre grupos e intra grupos. Un valor F grande indica variabilidad entre las medias.
    Análisis del estadístico F: Representa la razón de la variación entre grupos e intra grupos. Un valor F grande indica variabilidad entre las medias. Análisis del estadístico F: Representa la razón de la variación entre grupos e intra grupos. Un valor F grande indica variabilidad entre las medias.
    Interpretación del ANOVA

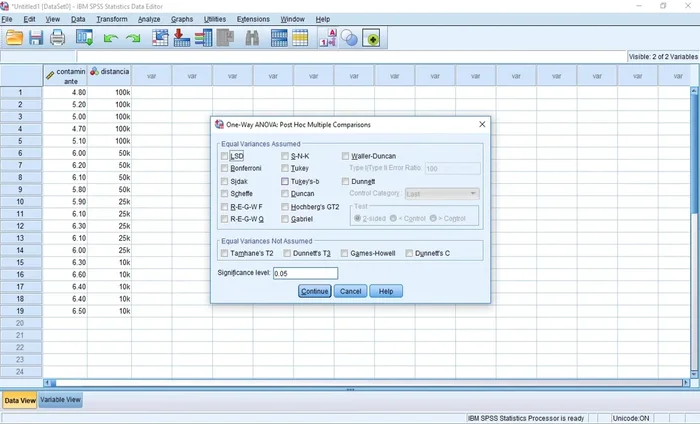
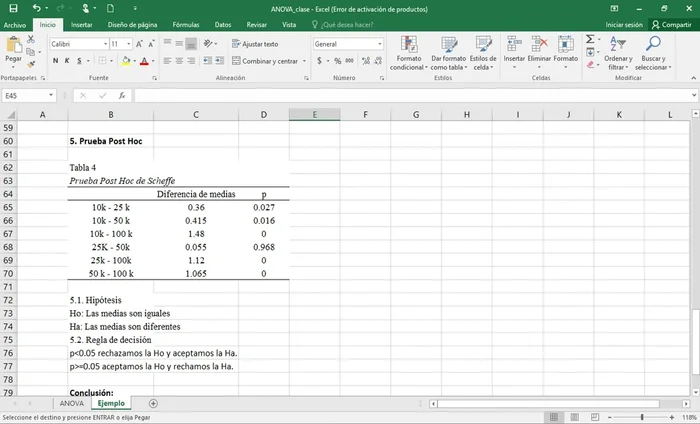
  5. Pruebas Post Hoc

    • Se utilizan para determinar qué grupos tienen medias significativamente diferentes. Se usa la prueba de Tukey (grupos de igual tamaño) o Games-Howell (grupos de distinto tamaño).
    Pruebas post hoc (si se rechaza H0): Se utilizan para determinar qué grupos tienen medias significativamente diferentes. Se usa la prueba de Tukey (grupos de igual tamaño) o Games-Howell (grupos de distinto tamaño).
    Pruebas Post Hoc

  6. Ejemplo Práctico en SPSS: Preparación

    • Análisis de la contaminación en un río a diferentes distancias.
    • Creación de variables (contaminante y distancia).
    Ingreso de datos en SPSS: Creación de variables (contaminante y distancia). Ingreso de datos en SPSS: Creación de variables (contaminante y distancia).
    Ejemplo Práctico en SPSS: Preparación

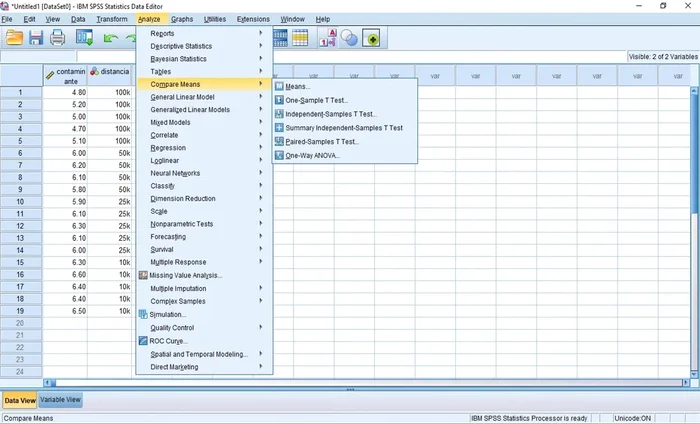
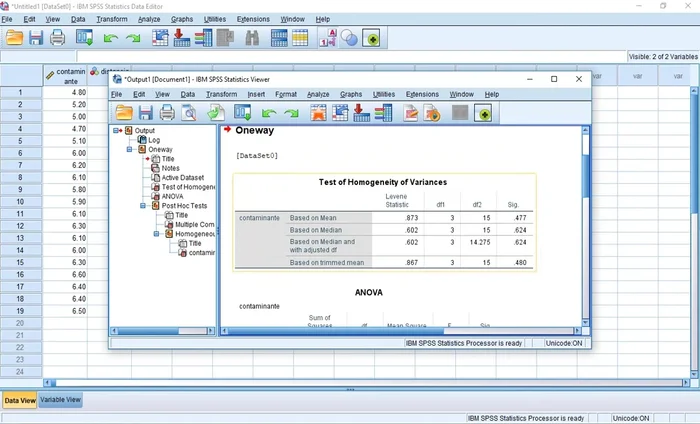
  7. Ejecución del ANOVA en SPSS

    • Analizar > Comparar medias > ANOVA de un factor.
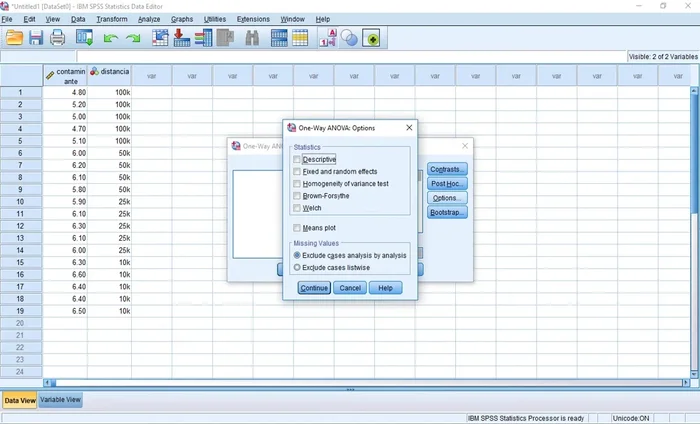
    • Prueba de Levene para la homogeneidad de varianzas (se usa la prueba de Brown-Forsythe si se viola la normalidad).
    • Seleccionar Games-Howell si los grupos tienen tamaños diferentes (como en este ejemplo).
    Prueba Post Hoc: Seleccionar Games-Howell si los grupos tienen tamaños diferentes (como en este ejemplo). Prueba Post Hoc: Seleccionar Games-Howell si los grupos tienen tamaños diferentes (como en este ejemplo). Prueba Post Hoc: Seleccionar Games-Howell si los grupos tienen tamaños diferentes (como en este ejemplo).
    Ejecución del ANOVA en SPSS

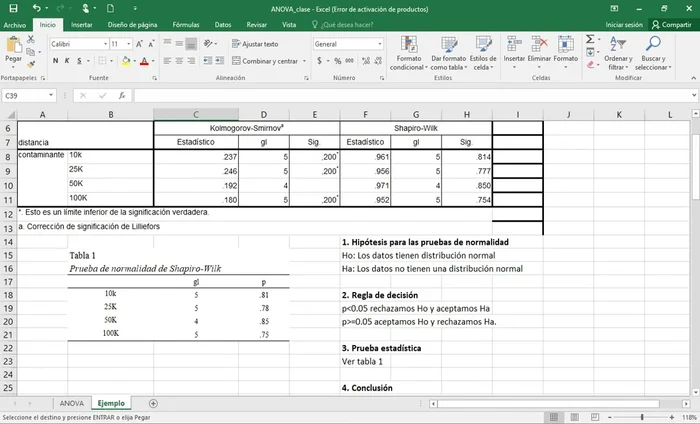
  8. Verificación de la Normalidad

    • se verifica si los datos cumplen con el supuesto de normalidad.
    Prueba de normalidad (Shapiro-Wilk): se verifica si los datos cumplen con el supuesto de normalidad.
    Verificación de la Normalidad

  9. Análisis e Interpretación de Resultados

    • análisis de la tabla ANOVA y de las pruebas post hoc.
    • Interpretación de los resultados del ANOVA y de las pruebas post hoc para determinar qué grupos presentan diferencias significativas en sus medias.
    Conclusión: Interpretación de los resultados del ANOVA y de las pruebas post hoc para determinar qué grupos presentan diferencias significativas en sus medias. Conclusión: Interpretación de los resultados del ANOVA y de las pruebas post hoc para determinar qué grupos presentan diferencias significativas en sus medias.
    Análisis e Interpretación de Resultados
[RelatedPost]

Tips

  • Asegurarse de cumplir los supuestos del ANOVA antes de realizar el análisis.
  • Utilizar la prueba post hoc adecuada según el tamaño de los grupos.
  • Interpretar cuidadosamente los resultados del valor p para tomar decisiones sobre las hipótesis.

Common Mistakes to Avoid

1. Violación de la normalidad de los residuos

Razón: Los datos no siguen una distribución normal, lo que afecta la validez de las pruebas F de ANOVA.
Solución: Transformar los datos o utilizar una prueba no paramétrica como la prueba de Kruskal-Wallis.

2. Desigualdad de varianzas (Heterocedasticidad)

Razón: Las varianzas de los grupos no son iguales, lo que puede sesgar los resultados del ANOVA.
Solución: Aplicar una prueba de ANOVA robusta a la heterocedasticidad, como el Welch ANOVA.

3. Independencia de las observaciones violada

Razón: Las observaciones dentro de los grupos no son independientes, por ejemplo, datos repetidos o correlacionados.
Solución: Utilizar un modelo estadístico que tenga en cuenta la dependencia entre las observaciones, como modelos mixtos.

FAQs

¿Qué pasa si no se cumplen los supuestos del ANOVA?
Si los supuestos de normalidad e igualdad de varianzas no se cumplen, existen alternativas no paramétricas como la prueba de Kruskal-Wallis. También se pueden aplicar transformaciones a los datos para intentar cumplir con los supuestos.
¿Cómo interpreto la significancia estadística (p-valor) en el ANOVA?
Un p-valor menor a 0.05 (usualmente) indica que existe una diferencia significativa entre al menos dos de las medias de los grupos. Un p-valor mayor a 0.05 sugiere que no hay evidencia suficiente para rechazar la hipótesis nula de que todas las medias son iguales.